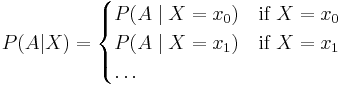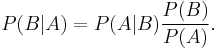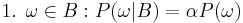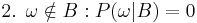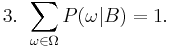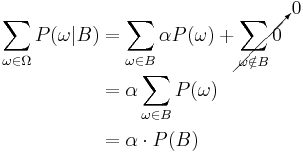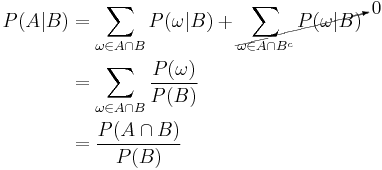Conditional probability
In probability theory, the "conditional probability of  given
given  " is the probability of
" is the probability of  if
if  is known to occur. It is commonly notated
is known to occur. It is commonly notated 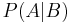 , and sometimes
, and sometimes 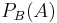 . (The vertical line should not be mistaken for logical OR.)
. (The vertical line should not be mistaken for logical OR.) 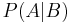 can be visualised as the probability of event
can be visualised as the probability of event  when the sample space is restricted to event
when the sample space is restricted to event  . Mathematically, it is defined for
. Mathematically, it is defined for 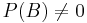 as
as
Formally, 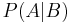 is defined as the probability of
is defined as the probability of  according to a new probability function on the sample space, such that outcomes not in
according to a new probability function on the sample space, such that outcomes not in  have probability 0 and that it is consistent with all original probability measures. The above definition follows (see Formal derivation).[1]
have probability 0 and that it is consistent with all original probability measures. The above definition follows (see Formal derivation).[1]
Contents |
Definition
Conditioning on an event
Given two events  and
and  in the same probability space with
in the same probability space with 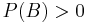 , the conditional probability of
, the conditional probability of  given
given  is defined as the quotient of the unconditional joint probability of
is defined as the quotient of the unconditional joint probability of  and
and  , and the unconditional probability of
, and the unconditional probability of  :
:
The above definition is how conditional probabilities are introduced by Kolmogorov. However, other authors such as De Finetti prefer to introduce conditional probability as an axiom of probability. Although mathematically equivalent, this may be preferred philosophically; under major probability interpretations such as the subjective theory, conditional probability is considered a primitive entity. Further, this "multiplication axiom" introduces a symmetry with the summation axiom[2]:
Multiplication axiom:
Summation axiom (A and B mutually exclusive):
Definition with σ-algebra
If 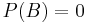 , then the simple definition of
, then the simple definition of 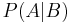 is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).
is undefined. However, it is possible to define a conditional probability with respect to a σ-algebra of such events (such as those arising from a continuous random variable).
For example, if X and Y are non-degenerate and jointly continuous random variables with density ƒX,Y(x, y) then, if B has positive measure,
The case where B has zero measure can only be dealt with directly in the case that B={y0}, representing a single point, in which case
If A has measure zero then the conditional probability is zero. An indication of why the more general case of zero measure cannot be dealt with in a similar way can be seen by noting that the limit, as all δyi approach zero, of
depends on their relationship as they approach zero. See conditional expectation for more information.
Conditioning on a random variable
Conditioning on an event may be generalized to conditioning on a random variable. Let  be a random variable taking some value from
be a random variable taking some value from 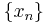 . Let
. Let  be an event. The probability of
be an event. The probability of  given
given  is defined as
is defined as
Note that 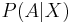 and
and  are now both random variables. From the law of total probability, the expected value of
are now both random variables. From the law of total probability, the expected value of 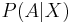 is equal to the unconditional probability of
is equal to the unconditional probability of  .
.
Example
Consider the rolling of two fair six-sided dice.
- Let
 be the value rolled on die 1
be the value rolled on die 1 - Let
 be the value rolled on die 2
be the value rolled on die 2 - Let
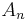 be the event that
be the event that 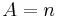
- Let
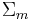 be the event that
be the event that 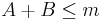
Suppose we roll  and
and  . What is the probability that
. What is the probability that 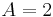 ? Table 1 shows the sample space.
? Table 1 shows the sample space. 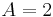 in 6 of the 36 outcomes, so
in 6 of the 36 outcomes, so 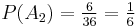 .
.
| + | B=1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A=1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Suppose however that somebody else rolls the dice in secret, revealing only that 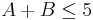 . Table 2 shows that
. Table 2 shows that 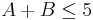 for 10 outcomes.
for 10 outcomes. 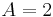 in 3 of these. The probability that
in 3 of these. The probability that 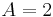 given that
given that 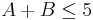 is therefore
is therefore 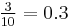 . This is a conditional probability, because it has a condition that limits the sample space. In more compact notation,
. This is a conditional probability, because it has a condition that limits the sample space. In more compact notation, 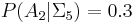 .
.
| + | B=1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A=1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Statistical independence
If two events  and
and  are statistically independent, the occurrence of
are statistically independent, the occurrence of  does not affect the probability of
does not affect the probability of  , and vice versa. That is,
, and vice versa. That is,
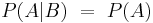
 .
.
Using the definition of conditional probability, it follows from either formula that
This is the definition of statistical independence. This form is the preferred definition, as it is symmetrical in  and
and  , and no values are undefined if
, and no values are undefined if 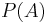 or
or 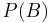 is 0.
is 0.
Common fallacies
Assuming conditional probability is of similar size to its inverse
In general, it cannot be assumed that 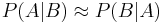 . This can be an insidious error, even for those who are highly conversant with statistics.[3] The relationship between
. This can be an insidious error, even for those who are highly conversant with statistics.[3] The relationship between 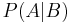 and
and 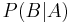 is given by Bayes' theorem:
is given by Bayes' theorem:
That is, 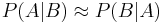 only if
only if 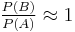 , or equivalently,
, or equivalently, 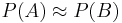 .
.
Assuming marginal and conditional probabilities are of similar size
In general, it cannot be assumed that 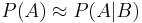 . These probabilities are linked through the formula for total probability:
. These probabilities are linked through the formula for total probability:
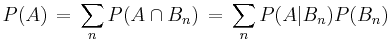 .
.
This fallacy may arise through selection bias.[4] For example, in the context of a medical claim, let 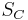 be the event that sequelae
be the event that sequelae  occurs as a consequence of circumstance
occurs as a consequence of circumstance  . Let
. Let  be the event that an individual seeks medical help. Suppose that in most cases,
be the event that an individual seeks medical help. Suppose that in most cases,  does not cause
does not cause  so
so 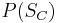 is low. Suppose also that medical attention is only sought if
is low. Suppose also that medical attention is only sought if  has occurred. From experience of patients, a doctor may therefore erroneously conclude that
has occurred. From experience of patients, a doctor may therefore erroneously conclude that 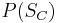 is high. The actual probability observed by the doctor is
is high. The actual probability observed by the doctor is 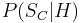 .
.
Formal derivation
This section is based on the derivation given in Grinsted and Snell's Introduction to Probability.[5]
Let  be a sample space with elementary events
be a sample space with elementary events 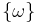 . Suppose we are told the event
. Suppose we are told the event 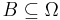 has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on
has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on 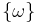 to reflect this. For events in
to reflect this. For events in  , It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor
, It is reasonable to assume that the relative magnitudes of the probabilities will be preserved. For some constant scale factor  , the new distribution will therefore satisfy:
, the new distribution will therefore satisfy:
Substituting 1 and 2 into 3 to select  :
:
So the new probability distribution is
Now for a general event  ,
,
See also
- Borel–Kolmogorov paradox
- Chain rule (probability)
- Posterior probability
- Conditioning (probability)
- Joint probability distribution
- Conditional probability distribution
- Class membership probabilities
References
- ^ George Casella and Roger L. Berger (1990), Statistical Inference, Duxbury Press, ISBN 0534119581 (p. 18 et seq.)
- ^ Gillies, Donald (2000); "Philosophical Theories of Probability"; Routledge; Chapter 4 "The subjective theory"
- ^ Paulos, J.A. (1988) Innumeracy: Mathematical Illiteracy and its Consequences, Hill and Wang. ISBN 0809074478 (p. 63 et seq.)
- ^ Thomas Bruss, F; Der Wyatt Earp Effekt; Spektrum der Wissenschaft; March 2007
- ^ Grinstead and Snell's Introduction to Probability, p. 134
External links
- Weisstein, Eric W., "Conditional Probability" from MathWorld.
- F. Thomas Bruss Der Wyatt-Earp-Effekt oder die betörende Macht kleiner Wahrscheinlichkeiten (in German), Spektrum der Wissenschaft (German Edition of Scientific American), Vol 2, 110–113, (2007).
- Conditional Probablity Problems with Solutions
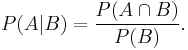
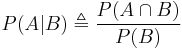
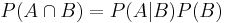
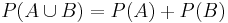
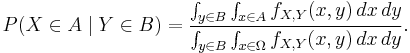
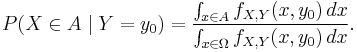
![P(X \in A \mid Y \in \cup_i[y_i,y_i%2B\delta y_i]) \approxeq
\frac{\sum_{i} \int_{x\in A} f_{X,Y}(x,y_i)\,dx\,\delta y_i}{\sum_{i}\int_{x\in\Omega} f_{X,Y}(x,y_i) \,dx\, \delta y_i} ,](/2012-wikipedia_en_all_nopic_01_2012/I/2dd41b1964098c5bce4df0a83a9c0ce0.png)